What I cannot code-up, I do not understand
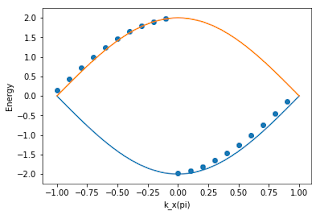
There you go! Paraphrasing Richard Feynman-- done! Google Summer of Code -- done! I have gained valuable experience from the internship. Also, I hope to become a part of QuTiP soon. The title of this post more or less sums up my experience from the program. This will be a poor man's version of Feynman's dying quotes(on his blackboard!) "What I cannot create, I do not understand" "Know how to solve every problem that has been solved." With some awesome guidance from my mentors, I have been able to simulate some very well known concepts of lattice physics. Recreating a problem gives me an immense satisfaction as well as the confidence of understanding a problem inside out. I have never been in the elite bracket of physicists who can solve any problem on a piece of paper or a board. I am a computational person. So, to me redoing a problem means coding it up on a computer. I daresay, the list of problems that I believe to understand well has grown con...